About the Project
Algorithm efficiency for computationally expensive objective functions (e.g. computer codes) is greatly improved with the use of statistically based surrogate response surfaces iteratively built during the search process and with intelligent algorithms that effectively utilize parallel and distributed computing.
The optimization and uncertainty quantification effort is used to improve model forecasts, and to have a tool for comparing alternative management practices, monitoring procedures, and design in water resources and other areas.
The research focuses on finding cost-effective, robust solutions for engineering problems by using computational mathematics for optimization, modeling and statistical analyses. This effort includes development of numerically efficient nonlinear optimization algorithms utilizing high performance computing (including asynchronous parallelism) and applications to data on complex, nonlinear environmental systems. The algorithms address local and global continuous and integer optimization, stochastic optimal control, and uncertainty quantification problems. In her recent research algorithms, efficiency is improved with the use of surrogate response surfaces iteratively built during the search process and with intelligent algorithms that effectively utilize parallel and distributed computing. The optimization and uncertainty quantification effort is used to improve model forecasts, to evaluate monitoring schemes and to have a tool for comparing alternative management practices. Algorithms that are efficient because they require relatively few simulations are essential for doing calibration and uncertainty analysis on computationally expensive engineering simulation models.
Optimization (for nonlinear inverse problems or for design/cost optimization) in engineering, natural sciences and economics can be coupled to a detailed numerical model f(x) describing the complex system of interest, where x ϵ D is a vector of decision variables or model parameter. This is called “Simulation-Optimization”. However, if the numerical model f(x) is somewhat “expensive” (e.g. CPU minutes to days for a single simulation evaluation) and nonconvex, then conventional optimization methods (e.g. derivative-based optimization or genetic algorithms) often cannot find good solutions within a feasible amount of time. This is because the computational expense of the simulation model severely limits the number of evaluations and access to derivative information. This is especially true if the function f(x) is multimodal (e.g. has multiple local minima), requires many hours or days per simulation, or if the goal is Multi-objective optimization or Uncertainty Quantification.
Surrogate Optimization involves the use of an iterative multivariate approximation of an expensive objective function (e.g.one based on a complex simulation model) to significantly reduce the number of simulations required to obtain accurate optimization solutions for a numerically defined function f(x). The methods described will solve problems with continuous and/or integer variables, single ormulti-objectives, and with local or global (e.g. multi-modal) optimization problems (with a focus on global optimization). We will consider error analysis of surrogate approximations and the use of ensembles (mixtures) of surrogate approximations in optimization search.
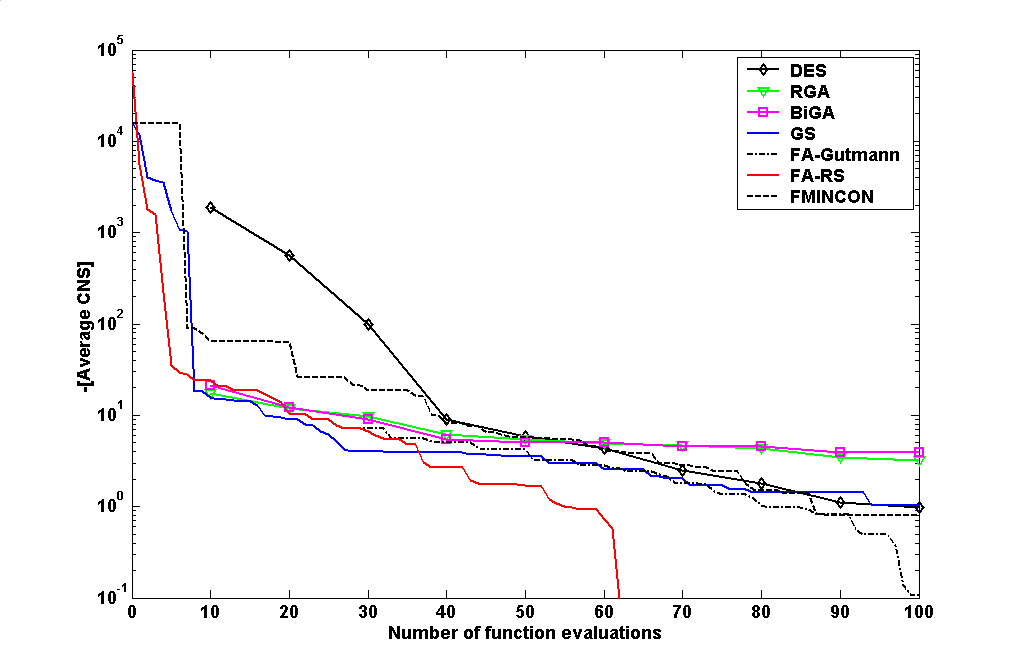
The Surrogate S(x) is a constantly updated approximation of the expensive function f(x) computed by fitting a response surface (e.g. a spline) to the point for f(xi) for all points xi for which the expensive simulation model has been evaluated in previous iterations of the search. The Surrogate S(x) can be very inexpensively evaluated at any point in D so it can be used to guide the optimization search. This can result in much more accurate solutions if the number of simulation is limited as shown for a minimization problem in Fig. 1 above.
