About the Project
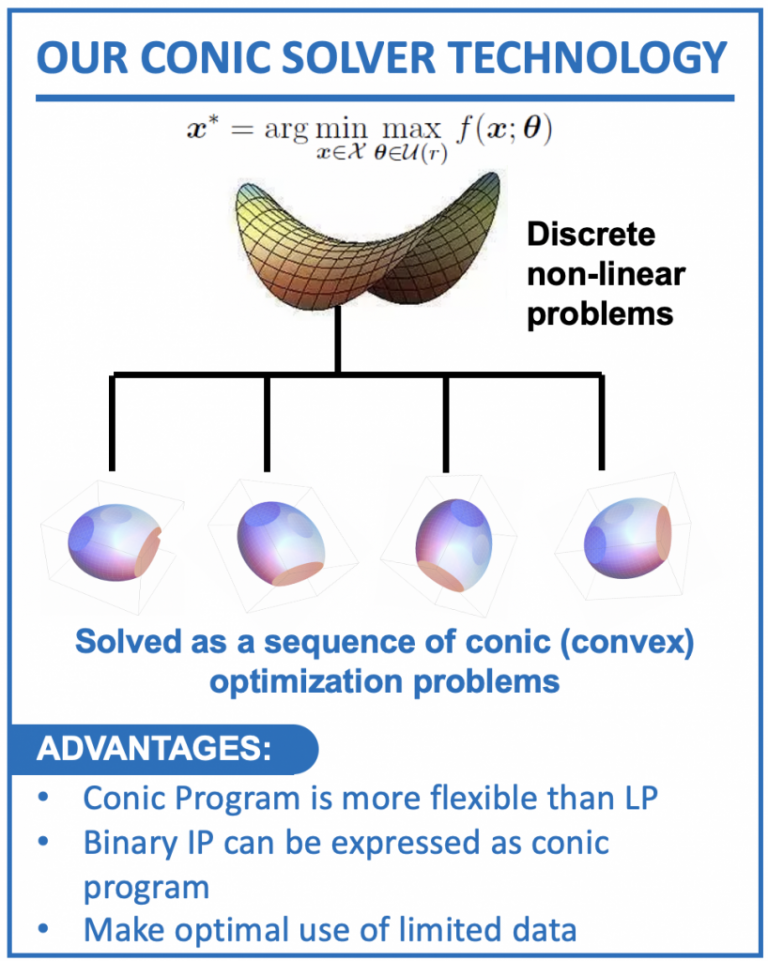
The problems that arise in the real world are difficult due to the inherent non linearities in the model. Academic groups from different schools have tackled these problems by linearizing and discretizing the model and data uncertainty. This allow them to solve the optimization problem as large scale mixed integer linear problems, using commercially available solvers like cplex and gurobi. Other groups like many in the CS field uses modern ML on huge amount of data to develop model free solutions to this problem. But both approaches have their limitations- MILP has only limited modelling power and quickly descend into huge scaling problem, whereas ML requires large amount of data to train to make effective decision.
Our approach will build on our strength in modelling and solving large scale prescriptive problems as convex conic programs, which is a better way to approximate discrete non-linear problems often encountered in this field. In this way, we use better model to ensure we make optimal use of even a small amount of data to make good decision. Of course the key is to develop good algorithms and theories to solve these problems.
The objective of this project led by Toh Kim Chuan along with Andrew Lim, Melvyn Sim and Teo Chung Piaw, is to develop new algorithms to solve some of these challenging conic programs. Packages developed by Kim Chuan, like SDPT3 and SDPNAL+, are now being used regularly in research labs all over the world to solve smaller scale problems.

The hope is to advance the theory further and develop them into industrial strength packages that can scale in performance. Along the way, we plan to incorporate B&B methodology into our solvers to deal with discrete constraints in the nonlinear problems, by exploiting specific problem structure such as block angular or small tree width settings. This approach has been very promising, and in one recent test case, we have been able to exploit the block angular structure in constraint matrix to develop a solution that is a few hundred times faster than commercial solver.
